En estadística y probabilidad se llama distribución normal,
distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua
que con más frecuencia aparece en fenómenos reales.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro. Esta curva se conoce como campana de Gauss.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística es un modelo matemático que sólo permite describir un fenómeno,
sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí
que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la
normal son:
La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.[1] Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".
En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.
Función de densidad
Se dice que una variable aleatoriacontinua X sigue una distribución normal de parámetros μ y σ y se denota X~N(μ, σ) si su función de densidad está dada por:

donde μ (mu) es la media y σ (sigma) es la desviación típica (σ2 es la varianza).[5]
Se llama distribución normal "estándar" a aquélla en la que sus parámetros toman los valores μ = 0 y σ = 1. En este caso la función de densidad tiene la siguiente expresión:

Su gráfica se muestra a la derecha y con frecuencia se usan tablas para el cálculo de los valores de su distribución.
Función de distribución
La función de distribución de la distribución normal está definida como sigue:

Por tanto, la función de distribución de la normal estándar es:
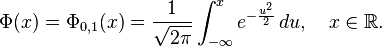
Esta función de distribución puede expresarse en términos de una función especial llamada función error de la siguiente forma:
![Phi(x)
=frac{1}{2} Bigl[ 1 + operatorname{erf} Bigl( frac{x}{sqrt{2}} Bigr) Bigr],
quad xinmathbb{R},](http://upload.wikimedia.org/math/0/0/3/003dabb870f6a1fc0521a85000ea8090.png)
y la propia función de distribución puede, por consiguiente, expresarse así:
![Phi_{mu,sigma^2}(x)
=frac{1}{2} Bigl[ 1 + operatorname{erf} Bigl( frac{x-mu}{sigmasqrt{2}} Bigr) Bigr],
quad xinmathbb{R}.](http://upload.wikimedia.org/math/3/5/3/3537f96b6dfa850f2e6fcb765a03c28c.png)
El complemento de la función de distribución de la normal estándar, 1 − Φ(x), se denota con frecuencia Q(x), y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.[6] [7] Esto representa la cola de probabilidad de la distribución gaussiana. También se usan ocasionalmente otras definiciones de la función Q, las cuales son todas
ellas transformaciones simples de Φ.[8]
La inversa de la función de distribución de la normal estándar (función cuantil) puede expresarse en términos de la inversa de la función de error:
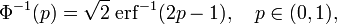
y la inversa de la función de distribución puede, por consiguiente, expresarse como:
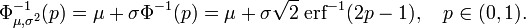
Esta función cuantil se llama a veces la función probit. No hay una primitiva elemental para la función probit. Esto no quiere decir meramente que no se conoce, sino que se ha probado la inexistencia de tal función. Existen varios métodos exactos para aproximar la función cuantil mediante la distribución normal (véase función cuantil).
Los valores Φ(x) pueden aproximarse con mucha precisión por distintos métodos, tales como integración numérica, series de Taylor, series asintóticas y fracciones continuas.
Límite inferior y superior estrictos para la función de distribución
Para grandes valores de x la función de distribución de la normal estándar 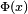 es muy próxima a 1 y
es muy próxima a 1 y  está muy cerca de 0. Los límites elementales
está muy cerca de 0. Los límites elementales

en términos de la densidad  son útiles.
son útiles.
Usando el cambio de variable v = u²/2, el límite superior se obtiene como sigue:

De forma similar, usando  y la regla del cociente,
y la regla del cociente,

Resolviendo para  proporciona el límite inferior.
proporciona el límite inferior.
Funciones generadoras
Función generadora de momentos
La función generadora de momentos se define como la esperanza de e(tX). Para una distribución normal, la función generadora de momentos es:
![M_X(t) = mathrm{E} left[ e^{tX} right] = int_{-infty}^{infty} frac{1}{sigma sqrt{2pi} } e^{-frac{(x - mu)^2}{2 sigma^2}} e^{tx} , dx = e^{mu t + frac{sigma^2 t^2}{2}}](http://upload.wikimedia.org/math/0/8/3/0833056dec593a5766850cf55e4923dd.png)
como puede comprobarse completando el cuadrado en el exponente.
Función característica
La función característica se define como la esperanza de eitX, donde i es la unidad imaginaria. De este modo, la función característica se obtiene reemplazando t por it en la función generadora de momentos.
Para una distribución normal, la función característica es[9]
![begin{align}
chi_X(t;mu,sigma) &{} = M_X(i t) = mathrm{E}
left[ e^{i t X} right]
&{}=
int_{-infty}^{infty}
frac{1}{sigma sqrt{2pi}}
e^{- frac{(x - mu)^2}{2sigma^2}}
e^{i t x}
, dx
&{}=
e^{i mu t - frac{sigma^2 t^2}{2}}
end{align}](http://upload.wikimedia.org/math/4/c/b/4cbace25f8080cfb3c00826417689533.png)
Propiedades
Algunas propiedades de la distribución normal son:
- Es simétrica respecto de su media, μ;

Distribución de probabilidad alrededor de la media en una distribución N(μ, σ).
- La moda y la mediana son ambas iguales a la media, μ;
- Los puntos de inflexión de la curva se dan para x = μ − σ y x = μ + σ.
- Distribución de probabilidad en un entorno de la media:
- en el intervalo [μ - σ, μ + σ] se encuentra comprendida, aproximadamente, el 68,26% de la distribución;
- en el intervalo [μ - 2σ, μ + 2σ] se encuentra, aproximadamente, el 95,44% de la distribución;
- por su parte, en el intervalo [μ -3σ, μ + 3σ] se encuentra comprendida, aproximadamente, el 99,74% de la distribución. Estas propiedades son de gran utilidad para el establecimiento de intervalos de confianza. Por otra parte, el hecho de que prácticamente la totalidad de la distribución se encuentre a tres desviaciones típicas de la media justifica los límites de las tablas empleadas habitualmente en la normal estándar.
- Si X ~ N(μ, σ2) y a y b son números reales, entonces (aX + b) ~ N(aμ+b, a2σ2).
- Si X ~ N(μx, σx2) e Y ~ N(μy, σy2) son variables aleatorias normales independientes, entonces:
- Su suma está normalmente distribuida con U = X + Y ~ N(μx + μy, σx2 + σy2) (demostración). Recíprocamente, si dos variables aleatorias independientes tienen una suma normalmente distribuida, deben ser normales (Teorema de Crámer).
- Su diferencia está normalmente distribuida con
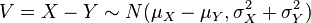 .
.
- Si las varianzas de X e Y son iguales, entonces U y V son independientes entre sí.
- La divergencia de Kullback-Leibler,
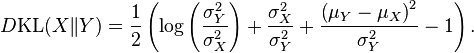
- Si
 e
e 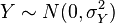 son variables aleatorias independientes normalmente distribuidas, entonces:
son variables aleatorias independientes normalmente distribuidas, entonces:
- Si
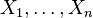 son variables normales estándar independientes, entonces
son variables normales estándar independientes, entonces 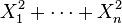 sigue una distribución χ² con n grados de libertad.
sigue una distribución χ² con n grados de libertad.
- Si
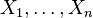 son variables normales estándar independientes, entonces la media muestral
son variables normales estándar independientes, entonces la media muestral  y la varianza muestral
y la varianza muestral 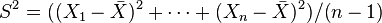 son independientes. Esta propiedad caracteriza a las distribuciones normales y contribuye a explicar por qué el test-F no es robusto respecto a la no-normalidad).
son independientes. Esta propiedad caracteriza a las distribuciones normales y contribuye a explicar por qué el test-F no es robusto respecto a la no-normalidad).
Estandarización de variables aleatorias normales
Como consecuencia de la Propiedad 1; es posible relacionar todas las variables aleatorias normales con la distribución normal estándar.
Si X ~ N(μ,σ2), entonces
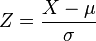
es una variable aleatoria normal estándar: Z ~ N(0,1).
La transformación de una distribución X ~ N(μ, σ) en una N(0, 1) se llama normalización, estandarización o tipificación de la variable X.
Una consecuencia importante de esto es que la función de distribución de una distribución normal es, por consiguiente,
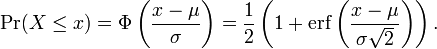
A la inversa, si Z es una distribución normal estándar, Z ~ N(0,1), entonces
- X = σZ + μ
es una variable aleatoria normal tipificada de media μ y varianza σ2.
La distribución normal estándar está tabulada (habitualmente en la forma de el valor de la función de distribución Φ) y las otras distribuciones normales pueden obtenerse como transformaciones simples, como se describe más arriba, de la distribución estándar. De este modo se pueden usar los valores tabulados de la función de distribución normal estándar para encontrar valores de la función de distribución de cualquier otra distribución normal.
Momentos
Los primeros momentos de la distribución normal son:
| Número |
Momento |
Momento central |
Cumulante |
| 0 |
1 |
1 |
|
| 1 |
μ |
0 |
μ |
| 2 |
μ2 + σ2 |
σ2 |
σ2 |
| 3 |
μ3 + 3μσ2 |
0 |
0 |
| 4 |
μ4 + 6μ2σ2 + 3σ4 |
3σ4 |
0 |
| 5 |
μ5 + 10μ3σ2 + 15μσ4 |
0 |
0 |
| 6 |
μ6 + 15μ4σ2 + 45μ2σ4 + 15σ6 |
15σ6 |
0 |
| 7 |
μ7 + 21μ5σ2 + 105μ3σ4 + 105μσ6 |
0 |
0 |
| 8 |
μ8 + 28μ6σ2 + 210μ4σ4 + 420μ2σ6 + 105σ8 |
105σ8 |
0 |
Todos los cumulantes de la distribución normal, más allá del segundo, son cero.
Los momentos centrales de orden superior (2k con μ = 0) vienen dados por la fórmula
![Eleft[X^{2k}right]=frac{(2k)!}{2^k k!} sigma^{2k}.](http://upload.wikimedia.org/math/9/e/e/9ee2fb62550523bac223697b7ad104b0.png)
El Teorema del Límite Central
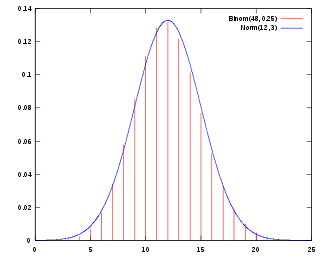
Gráfica de la función de distribución de una normal con μ = 12 y σ = 3, aproximando la función de distribución de una binomial con n = 48 y p = 1/4
El Teorema del límite central establece que bajo ciertas condiciones (como pueden ser independientes e idénticamente distribuidas con varianza finita), la suma de un gran número
de variables aleatorias se distribuye aproximadamente como una normal.
La importancia práctica del Teorema del límite central es que la función de distribución de la normal puede usarse como aproximación de algunas otras funciones de distribución. Por ejemplo:
- Una distribución binomial de parámetros n y p es aproximadamente normal para grandes valores de n, y p no demasiado cercano a 1 ó 0 (algunos libros recomiendan usar esta aproximación sólo si np y n(1 − p) son ambos, al menos, 5; en este caso se debería aplicar una corrección de continuidad).
La normal aproximada tiene parámetros μ = np, σ2 = np(1 − p).
- Una distribución de Poisson con parámetro λ es aproximadamente normal para grandes valores de λ.
La distribución normal aproximada tiene parámetros μ = σ2 = λ.
La exactitud de estas aproximaciones depende del propósito para el que se necesiten y de la tasa de convergencia a la distribución normal. Se da el caso típico de que tales aproximaciones son menos precisas en las colas de la distribución. El Teorema de Berry-Esséen proporciona un límite superior general del error de aproximación de la función de distribución.
Divisibilidad infinita
Las normales tienen una distribución de probabilidad infinitamente divisible: dada una
media μ, una varianza σ 2 ≥ 0, y un número natural n, la suma X1 + . . . + Xn de n variables aleatorias independientes

tiene esta específica distribución normal (para verificarlo, úsese la función característica de convolución y la inducción matemática).
Estabilidad
Las distribuciones normales son estrictamente estables.
Desviación típica e intervalos de confianza
Alrededor del 68% de los valores de una distribución normal están a una distancia σ > 1 (desviación típica) de la media, μ; alrededor del 95% de los valores están a dos desviaciones típicas de la media y alrededor del 99,7% están a tres desviaciones típicas de la media. Esto se conoce como la "regla 68-95-99,7" o la "regla empírica".
Para ser más precisos, el área bajo la curva campana entre μ − nσ y μ + nσ en términos de la función de distribución normal viene dada por

donde erf es la función error. Con 12 decimales, los valores para los puntos 1-, 2-, hasta 6-σ son:
 |
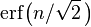 |
| 1 |
0,682689492137 |
| 2 |
0,954499736104 |
| 3 |
0,997300203937 |
| 4 |
0,999936657516 |
| 5 |
0,999999426697 |
| 6 |
0,999999998027 |
La siguiente tabla proporciona la relación inversa de múltiples σ correspondientes a unos pocos valores usados con frecuencia para el área bajo la campana de Gauss. Estos valores son útiles para determinar intervalos de confianza para los niveles especificados basados en una curva normalmente distribuida (o estimadoresasintóticamente normales):
 |
 |
| 0,80 |
1,28155 |
| 0,90 |
1,64485 |
| 0,95 |
1,95996 |
| 0,98 |
2,32635 |
| 0,99 |
2,57583 |
| 0,995 |
2,80703 |
| 0,998 |
3,09023 |
| 0,999 |
3,29052 |
| 0,9999 |
3,8906 |
| 0,99999 |
4,4172 |
donde el valor a la izquierda de la tabla es la proporción de valores que caerán en el intervalo dado y n es un múltiplo de la desviación típica que determina la anchura de el intervalo.
Forma familia exponencial
La distribución normal tiene forma de familia exponencial biparamétrica con dos parámetros naturales, μ y 1/σ2, y estadísticos naturales X y X2. La forma canónica tiene como parámetros 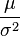 y
y  y estadísticos suficientes
y estadísticos suficientes 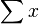 y
y 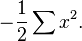
Distribución normal compleja
Considérese la variable aleatoria compleja gaussiana

donde X e Y son variables gaussianas reales e independientes con igual varianza  . La función de distribución de la variable conjunta es entonces
. La función de distribución de la variable conjunta es entonces
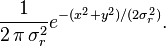
Como  , la función de distribución resultante para la variable gaussiana compleja Z es
, la función de distribución resultante para la variable gaussiana compleja Z es
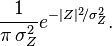
Distribuciones relacionadas
- Y˜Cauchy(μ = 0,θ = 1) es una distribución de Cauchy si Y = X1 / X2 para X1˜N(0,1) y X2˜N(0,1) son dos distribuciones normales independientes.
- Distribución normal truncada. si
 entonces truncando X por debajo de A y por encima de B dará lugar a una variable aleatoria de media
entonces truncando X por debajo de A y por encima de B dará lugar a una variable aleatoria de media  donde
donde 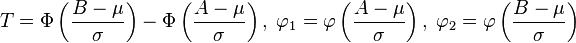
- y
 es la función de densidad de una variable normal estándar.
es la función de densidad de una variable normal estándar.
Estadística descriptiva e inferencial
Resultados
De la distribución normal se derivan muchos resultados, incluyendo rangos de percentiles ("percentiles" o "cuantiles"), curvas normales equivalentes, stanines, z-scores, y T-scores. Además, un número de procedimientos de estadísticos de comportamiento están basados en la asunción de que esos resultados están normalmente distribuidos. Por ejemplo, el test de Student y el análisis de varianza (ANOVA) (véase más abajo). La gradación de la curva campana asigna grados relativos basados en una distribución normal de resultados.
Tests de normalidad
Los tests de normalidad se aplican a conjuntos de datos para determinar su similitud con una distribución normal. La hipótesis nula es, en estos casos, si el conjunto de datos es similar a una distribución normal, por lo que un P-valor suficientemente pequeño indica datos no normales.
Estimación de parámetros
Estimación de parámetros de máxima verosimilitud
Supóngase que
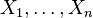
son independientes y cada una está normalmente distribuida con media μ y varianza σ 2 > 0. En términos estadísticos los valores observados de estas n variables aleatorias constituyen una "muestra de tamaño n de una población normalmente distribuida. Se desea estimar la media poblacional μ y la desviación típica poblacional σ, basándose en las valores observados de esta muestra. La función de densidad conjunta de estas n variables aleatorias independientes es
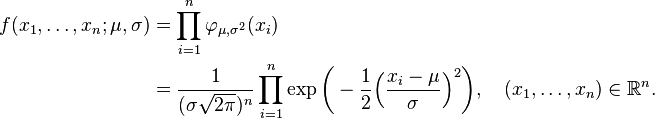
Como función de μ y σ, la función de verosimilitud basada en las observaciones X1, ..., Xn es
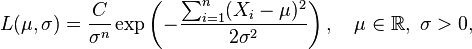
con alguna constante C > 0 (de la cual, en general, se permitiría incluso que dependiera de X1, ..., Xn, aunque desapareciera con las derivadas parciales de la función de log-verosimilitud respecto a los parámetros tenidos en cuenta, véase más abajo).
En el método de máxima verosimilitud, los valores de μ y σ que maximizan la función de verosimilitud se toman como estimadores de los parámetros poblacionales μ y σ.
Habitualmente en la maximización de una función de dos variables, se podrían considerar derivadas parciales. Pero aquí se explota el hecho de que el valor de μ que maximiza la función de verosimilitud con σ fijo no depende de σ. No obstante, encontramos que ese valor de μ, entonces se sustituye por μ en la función de verosimilitud y finalmente encontramos el valor de σ que maximiza la expresión resultante.
Es evidente que la función de verosimilitud es una función decreciente de la suma
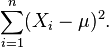
Así que se desea el valor de μ que minimiza esta suma. Sea

la media muestral basada en las n observaciones. Nótese que
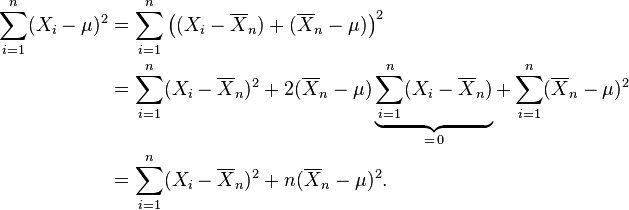
Sólo el último término depende de μ y se minimiza por

Esta es la estimación de máxima verosimilitud de μ basada en las n
observaciones X1, ..., Xn. Cuando sustituimos esta estimación por μ en la función de verosimilitud, obtenemos

Se conviene en denotar la "log-función de verosimilitud", esto es, el logaritmo de la función de verosimilitud, con una minúscula ℓ, y tenemos
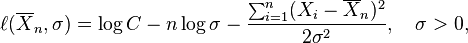
entonces
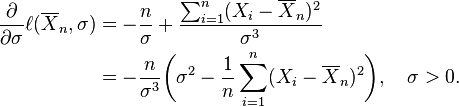
Esta derivada es positiva, cero o negativa según σ2 esté entre 0 y

o sea igual a esa cantidad, o mayor que esa cantidad. (Si hay solamente una observación, lo que significa que n = 1, o si X1 = ... = Xn, lo cual sólo ocurre con probabilidad cero, entonces 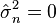 por esta fórmula, refleja el hecho de que en estos casos la función de verosimilitud es ilimitada cuando σ decrece hasta cero.)
por esta fórmula, refleja el hecho de que en estos casos la función de verosimilitud es ilimitada cuando σ decrece hasta cero.)
Consecuentemente esta media de cuadrados de residuos es el estimador de máxima verosimilitud de σ2, y su raíz cuadrada es el estimador de máxima verosimilitud de σ basado en las n observaciones. Este estimador 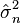 es sesgado, pero tiene un menor error medio al cuadrado que el habitual estimador insesgado, que es n/(n − 1) veces este estimador.
es sesgado, pero tiene un menor error medio al cuadrado que el habitual estimador insesgado, que es n/(n − 1) veces este estimador.
Sorprendente generalización
La derivada del estimador de máxima verosimilitud de la matriz de covarianza de una distribución normal multivariante es despreciable. Involucra el teorema espectral y la razón por la que puede ser mejor para ver un escalar como la traza de una matriz 1×1 matrix que como un mero escalar. Véase estimación de la covarianza de matrices.
Estimación insesgada de parámetros
El estimador  de máxima verosimilitud de la media poblacional μ, es un estimador insesgado de la media poblacional.
de máxima verosimilitud de la media poblacional μ, es un estimador insesgado de la media poblacional.
El estimador de máxima verosimilitud de la varianza es insesgado si asumimos que la media de la población es conocida a priori, pero en la práctica esto no ocurre. Cuando disponemos de una muestra y no sabemos nada de la media o la varianza de la población de la que se ha extraído, como se asumía en la derivada de máxima verosimilitud de arriba, entonces el estimador de máxima verosimilitud de la varianza es sesgado. Un estimador insesgado de la varianza σ2 es la cuasi varianza muestral:

que sigue una distribución Gamma cuando las Xi son normales independientes e idénticamente distribuidas:

con media 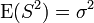 y varianza
y varianza 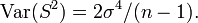
La estimación de máxima verosimilitud de la desviación típica es la raíz cuadrada de la estimación de máxima verosimilitud de la varianza. No obstante, ni ésta, ni la raíz cuadrada de la cuasivarianza muestral proporcionan un estimador insesgado para la desviación típica (véase estimación insesgada de la desviación típica para una fórmula particular para la distribución normal.
5.- Distribución gamma
En estadística la distribución gamma es una distribución de probabilidad continua con dos parámetros k y λ cuya función de densidad para valores x > 0 es
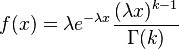
Aquí e es el número e y Γ es la función gamma. Para valores  la aquella es Γ(k) = (k − 1)! (el factorial de k − 1). En este caso - por ejemplo para describir un proceso de Poisson - se llaman la distribición distribución Erlang con un parámetro θ = 1 / λ.
la aquella es Γ(k) = (k − 1)! (el factorial de k − 1). En este caso - por ejemplo para describir un proceso de Poisson - se llaman la distribición distribución Erlang con un parámetro θ = 1 / λ.
El valor esperado y la varianza de una variable aleatoria X de distribución gamma son
- E[X] = k / λ = kθ
- V[X] = k / λ2 = kθ2
Relaciones
El tiempo hasta que el suceso número k ocurre en un Proceso de Poisson de intensidad λ es una variable aleatoria con distribución gamma. Eso es la suma de k variables aleatorias independientes de distribución exponencial con parámetro λ.
6.-Distribución beta
En estadística la distribución beta es una distribución de probabilidad continua con dos parámetros a y b cuya función de densidad para valores 0 < x < 1 es

Aquí Γ es la función gamma.
El valor esperado y la varianza de una variable aleatoria X con distribución beta son
![E[X]=frac{a}{a+b}](http://upload.wikimedia.org/math/0/7/7/077871166dae78e2b2176225958f3c68.png)
![V[X]=frac{ab}{(a+b+1)(a+b)^2}](http://upload.wikimedia.org/math/8/f/8/8f824697b17ca3dc6da90fd3a771d8c4.png) .
.
Un caso especial de la distribución beta con a = 1 y b = 1 es la distribución uniforme en el intervalo [0, 1].
Para relacionar con la muestra se iguala E[X] a la media y V[X] a la varianza y de despejan a
y b.