DISTRIBUCIONES DE LA
VARIABLE DISCRETA

Se denomina distribución de variable discreta a aquella 
cuya función de probabilidad sólo toma valores positivos en un conjunto 
de valores de  $X$  finito o infinito numerable. A dicha función se le llama
 función de masa de probabilidad. En este caso la distribución de
 probabilidad es el sumatorio de la función de masa, por lo que tenemos 
entonces que:

Y, tal como corresponde a la definición de distribución de probabilidad, esta expresión representa la suma de todas las probabilidades desde $-infty$ hasta el valor $x$ .

1.- Distribución binomial

Distribución binomial
Función de probabilidad
Función de distribución de probabilidad
Parámetros	$n geq 0$ número de ensayos (entero) $0leq p leq 1$ probabilidad de éxito (real)
Dominio	$k in {0,dots,n}!$
Función de probabilidad (fp)	${nchoose k} p^k (1-p)^{n-k} !$
Función de distribución (cdf)	$I_{1-p}(n-lfloor krfloor, 1+lfloor krfloor) !$
Media	$np!$
Mediana	Uno de ${lfloor nprfloor, lceil np rceil}$ ^[1]
Moda	$lfloor (n+1),prfloor!$
Varianza	$np(1-p)!$
Coeficiente de simetría	$frac{1-2p}{sqrt{np(1-p)}}!$
Curtosis	$frac{1-6p(1-p)}{np(1-p)}!$
Entropía	$frac{1}{2} ln left( 2 pi n e p (1-p) right) + O left( frac{1}{n} right)$
Función generadora de momentos (mgf)	$(1-p + pe^t)^n !$
Función característica	$(1-p + pe^{it})^n !$

En estadística, la distribución binomial es una distribución de probabilidad discreta que mide el número de éxitos en una secuencia de n ensayos independientes de Bernoulli con una probabilidad fija p de ocurrencia del éxito entre los ensayos.

Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.

Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:

$X sim B(n, p),$

La distribución binomial es la base del test binomial de significación estadística.

Ejemplos

Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:

Se lanza un dado un millon de veces y se cuenta el número X de tres obtenidos: entonces X ~ B(10, 1/6)
Se lanza una moneda dos veces y se cuenta el número X de caras obtenidas: entonces X ~ B(2, 1/2)
Una partícula se mueve unidimensionalmente con probabilidad q de moverse de aqui para allá y 1-q de moverse de allá para acá

Experimento Binomial

Existen muchas situaciones en las que se presenta una experiencia binomial. Cada uno de los experimentos es independiente de los restantes (la probabilidad del resultado de un experimento no depende del resultado del resto). El resultado de cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y fracaso). Las probabilidades de ambas posibilidades han de ser constantes en todos los experimentos (se denotan como p y q o p y 1-p).

Se designa por X a la variable que mide el número de éxitos que se han producido en los n experimentos.

Cuando se dan estas circunstancias, se dice que la variable sexo sigue una distribución de probabilidad binomial, y se denota B(n,p).

Características analíticas

Su función de probabilidad es

$!f(x)={n choose x}p^x(1-p)^{n-x} ,!$

donde $x = {0, 1, 2, dots , n},$

siendo $!{n choose x} = frac{n!}{x!(n-x)!} ,!$ las combinaciones de $n ,!$ en $x ,!$ ( $n ,!$ elementos tomados de $x ,!$ en $x ,!$ )

Ejemplo

Supongamos que se lanza un dado 50 veces y queremos la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una X ~ B(50, 1/6) y la probabilidad sería P(X=20):

$!P(X=20)={50 choose 20}(1/6)^{20}(1-1/6)^{50-20} ,!$

Propiedades características

$mathbb{E}[X] = np,$

$text{Var}[X] =np(1-p),$

Relaciones con otras variables aleatorias

Si $n$ tiende a infinito y $p$ es tal que producto entre ambos parámetros tiende a $lambda ,!$ , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro $λ$ .

Por último, se cumple que cuando n es muy grande (usualmente se exige que $n geq 30$ ) la distribución binomial puede aproximarse mediante la distribución anormal.

Propiedades reproductivas

Dadas n variables binomiales independientes, de parámetros n_i (i = 1,..., n) y $p$ , su suma es también una variable binomial, de parámetros n₁+... + n_n, y $p$ , es decir,

$Y = sum^{n}_{i = 1} X_i sim B(sum^{n}_{i = 1} n_i, p),$

2.- Distribución binomial negativa

Binomial negativa
Función de probabilidad La línea roja representa la media, y la verde tiene una longitud de aproximadamente 2σ.
Función de distribución de probabilidad
Parámetros	$r > 0!$ (real) $0<p<1!$ (real)
Dominio	$k in {0,1,2,ldots}!$
Función de probabilidad (fp)	$frac{Gamma(r+k)}{k!,Gamma(r)},p^r,(1-p)^k !$
Función de distribución (cdf)	$I p (r, k + 1) donde I p (x, y)$ es la función beta incompleta regularizada
Media	$r,frac{1-p}{p}$
Mediana
Moda	$lfloor(r-1),(1-p)/prfloortext{ si }r>1$ $0text{ si }rleq 1$
Varianza	$r,frac{1-p}{p^2}$
Coeficiente de simetría	$frac{2-p}{sqrt{r,(1-p)}}!$
Curtosis	$frac{6}{r} + frac{p^2}{r,(1-p)}!$
Entropía
Función generadora de momentos (mgf)	$left(frac{p}{1-(1-p) e^t}right)^r !$
Función característica	$left(frac{p}{1-(1-p) e^{i,t}}right)^r !$

En estadística la distribución binomial negativa es una distribución de probabilidad discreta que incluye a la distribución de Pascal.

El número de experimentos de Bernoulli de parámetro $θ$ independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y $θ$ .

La distribución geométrica es el caso concreto de la binomial negativa cuando k = 1.

Propiedades

Su función de probabilidad es

$! b^*(x;k,theta) = {x-1 choose k-1}theta^k(1-theta)^{x-k}$

para enteros x mayores o iguales que k, donde

$!{x-1 choose k-1} = frac{(x-1)!}{(k-1)!(x-k)!}$ .

Su media es

$!mu = frac{{k(1 - theta )}}{theta}$

si se piensa en el número de fracasos únicamente y

$!mu = frac{{k}}{theta}$

si se cuentan también los k-1 éxitos.

Su varianza es

$!sigma ^2 = frac{{k(1 - theta )}}{{theta ^2 }}$

en ambos casos.

Ejemplos

Si la probabilidad de que un niño expuesto a una enfermedad contagiosa la contraiga es 0,40, ¿cuál es la probabilidad de que el décimo niño expuesto a la enfermedad sea el tercero en contraerla? En este caso, X es el número de niños expuestos la enfermedad y

$!x = 10, k = 3, theta = 0,!40$

La solución es:

$!b^*(10;3,0,!4)={10-1 choose 3-1}0,!4^3(1-0,!4)^{10-3}={9 choose 2}0,!4^3(0,,6)^{7}=0,!0645$

En un proceso de manufactura se sabe que un promedio de1 en cada 10 productos es defectuoso, ¿cual es la probabilidad que el quinto (5) articulo examinado sea el tercero (3) en estar defectuoso?. La solucion es: X= articulos defectuosos P= 1/10 = 0,1 q= 1- 0,1 = 0,9 x= 5 ensayos K= 1 b*(5;1,0.1)=(5-11-1)(0.1)^1*(0.9)^5-1= b*(5;1,0.1)= 6.6% de probabilidad que el quinto elemento extraido sea el primero en estar defectuoso.

3.- Distribución de Poisson

**Distribucion De Poisson**
Función de probabilidad El eje horizontal es el índice k. La función solamente está definida en valores enteros de k. Las líneas que conectan los puntos son solo guías para el ojo y no indican continuidad.
Función de distribución de probabilidad El eje horizontal es el índice k.
Parámetros	$lambda in (0,infty)$
Dominio	$k in {0,1,2,ldots}$
Función de probabilidad (fp)	$frac{e^{-lambda} lambda^k}{k!}!$
Función de distribución (cdf)	$frac{Gamma(lfloor k+1rfloor, lambda)}{lfloor krfloor !}!text{ for }kge 0$ (dónde $Γ(x, y)$ es la Función gamma incompleta)
Media	$lambda,$
Mediana	$text{usualmente cerca de }lfloorlambda+1/3-0.02/lambdarfloor$
Moda	$lfloorlambdarfloortext{ (con }lambda-1text{ si }lambdatext{ es un entero)}$
Varianza	$lambda,$
Coeficiente de simetría	$lambda^{-1/2},$
Curtosis	$3+lambda^{-1},$
Entropía	$lambda[1!-!ln(lambda)]!+!e^{-lambda}sum_{k=0}^infty frac{lambda^kln(k!)}{k!}$
Función generadora de momentos (mgf)	$exp(lambda (e^t-1)),$
Función característica	$exp(lambda (e^{it}-1)),$

En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa la probabilidad que un determinado número de eventos ocurran en un determinado periodo de tiempo, dada una frecuencia media conocida e independientemente del tiempo discurrido desde el último evento.

Fue descubierta por Siméon-Denis Poisson, que la dio a conocer en 1838 en su trabajo Recherches sur la probabilité des jugements en matières criminelles et matière civile (Investigación sobre la probabilidad de los juicios en materias criminales y civiles).

Propiedades

La función de masa de la distribución de Poisson es

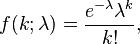
$f(k;lambda)=frac{e^{-lambda} lambda^k}{k!},,!$

donde

k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
λ es un parámetro positivo que representa el número de veces que se espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.
e es la base de los logaritmos naturales (e = 2,71828 ...)

Tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos de orden superior son polinomios de Touchard en λ cuyos coeficientes tienen una interpretación combinatorio. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el n-ésimo momento iguala al número de particiones de tamaño n.

La moda de una variable aleatoria de distribución de Poisson con un λ no entero es igual a 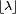$scriptstylelfloor lambda rfloor$ , el mayor de los enteros menores que λ (los símbolos $scriptstylelfloor rfloor$ representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.

La función generadora de momentos de la distribución de Poisson con valor esperado λ es

$mathrm{E}left(e^{tX}right)=sum_{k=0}^infty e^{tk} f(k;lambda)=sum_{k=0}^infty e^{tk} {lambda^k e^{-lambda} over k!} =e^{lambda(e^t-1)}.$

Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.

La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro λ₀ a otra de parámetro λ es

$D_{mathrm{KL}}(lambda||lambda_0) = lambda left( 1 - frac{lambda_0}{lambda} + frac{lambda_0}{lambda} log frac{lambda_0}{lambda} right).$

Relación con otras distribuciones

Sumas de variables aleatorias de Poisson

La suma de variables aleatorias de Poisson independientes es otra variable aleatoria de Poisson cuyo parámetro es la suma de los parámetros de las originales. Dicho de otra manera, si

$X_i sim mathrm{Poi}(lambda_i),, i=1,dots, N$

son N variables aleatorias de Poisson independientes, entonces

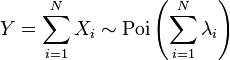$Y = sum_{i=1}^N X_i sim mathrm{Poi}left(sum_{i=1}^N lambda_iright),$ .

Distribución binomial

La distribución de Poisson es el caso límite de la distribución binomial. De hecho, si los parámetros n y $θ$ de una distribución binomial tienden a infinito de manera que $!lambda=ntheta$ se mantenga constante, la distribución límite obtenida es de Poisson.

Aproximación normal

Como consecuencia del teorema central del límite, para valores grandes de $λ$ , una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente

$Y = frac{X - lambda}{sqrt{lambda}}$

converge a una distribución normal de media nula y varianza 1.

Distribución exponencial

Supóngase que para cada valor t > 0, que representa el tiempo, el número de sucesos de cierto fenómeno aleatorio sigue una distribución de Poisson de parámetro λt. Entonces, los tiempos discurridos entre dos sucesos sucesivos sigue la distribución exponencial.

Ejemplos

Si el 2% de los libros encuadernados en cierto taller tiene encuadernación defectuosa, para obtener la probabilidad de que 5 de 400 libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson. En este caso concreto, k es 5 y , λ, el valor esperado de libros defectuosos es el 2% de 400, es decir, 8. Por lo tanto, la probabilidad buscada es

$!P(5;8)= frac{8^5e^{-8}}{5!}=0,092.$

Este problema también podría resolverse recurriendo a una distribución binomial de parámetros k = 5, n = 400 y $θ$ =0,02.

Procesos de Poisson

La distribución de Poisson se aplica a varios fenómenos discretos de la naturaleza (esto es, aquellos fenómenos que ocurren 0, 1, 2, 3,... veces durante un periodo definido de tiempo o en un área determinada) cuando la probabilidad de ocurrencia del fenómeno es constante en el tiempo o el espacio. Ejemplos de estos eventos que pueden ser modelados por la distribución de Poisson incluyen:

El número de autos que pasan a través de un cierto punto en una ruta (suficientemente distantes de los semáforos) durante un periodo definido de tiempo.
El número de errores de ortografía que uno comete al escribir una única página.
El número de llamadas telefónicas en una central telefónica por minuto.
El número de servidores web accedidos por minuto.
El número de animales muertos encontrados por unidad de longitud de ruta.
El número de mutaciones de determinada cadena de ADN después de cierta cantidad de radiación.
El número de núcleos atómicos inestables que decayeron en un determinado período en una porción de sustancia radiactiva. La radiactividad de la sustancia se debilitará con el tiempo, por lo tanto el tiempo total del intervalo usado en el modelo debe ser significativamente menor que la vida media de la sustancia.
El número de estrellas en un determinado volumen de espacio.
La distribución de receptores visuales en la retina del ojo humano.
La inventiva de un inventor a lo largo de su carrera.

4.-Distribución geométrica

En teoría de probabilidad y estadística, la distribución geométrica es cualquiera de las dos distribuciones de probabilidad discretas siguientes:

la distribución de probabilidad del número X del ensayo de Bernoulli necesaria para obtener un éxito, contenido en el conjunto { 1, 2, 3,...} o
la distribución de probabilidad del número Y = X − 1 de fallos antes del primer éxito, contenido en el conjunto { 0, 1, 2, 3,... }.

Cual de éstas es la que uno llama "la" distribución geométrica, es una cuestión de convención y conveniencia.

Propiedades

Si la probabilidad de éxito en cada ensayo es p, entonces la probabilidad de que x ensayos sean necesarios para obtener un éxito es

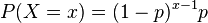
$P(X = x) = (1 - p)^{x-1}p,$

para x = 1, 2, 3,.... Equivalentemente, la probabilidad de que haya x fallos antes del primer éxito es

$P(Y=x) = (1 - p)^{x} p,$

para x = 0,1, 2, 3,....

En ambos casos, la secuencia de probabilidades es una progresión geométrica.

El valor esperado de una variable aleatoria X distribuida geométricamente es

$E(X) = frac{1}{p}.$

y dado que Y = X-1,

$E(Y) = frac{1-p}{p}.$

En ambos casos, la varianza es

$mbox{var}(Y) = mbox{var}(X) = frac{1-p}{p^2}.$

Las funciones generatrices de probabilidad de X y la de Y son, respectivamente,

$G_X(s) = frac{sp}{1-s(1-p)} quad textrm{y} quad G_Y(s) = frac{p}{1-s(1-p)}, quad |s| < (1-p)^{-1}.$

Como su análoga continua, la distribución exponencial, la distribución geométrica carece de memoria. Esto significa que si intentamos repetir el experimento hasta el primer éxito, entonces, dado que el primer éxito todavía no ha ocurrido, la distribución de probabilidad condicional del número de ensayos adicionales no depende de cuantos fallos se hayan observado. El dado o la moneda que uno lanza no tiene "memoria" de estos fallos. La distribución geométrica es de hecho la única distribución discreta sin memoria.

De todas estas distribuciones de probabilidad contenidas en {1, 2, 3,... } con un valor esperado dado μ, la distribución geométrica X con parámetro p = 1/μ es la de mayor entropía.

La distribución geométrica del número y de fallos antes del primer éxito es infinitamente divisible, esto es, para cualquier entero positivo n, existen variables aleatorias independientes Y ₁,..., Y_n distribuidas idénticamente la suma de las cuales tiene la misma distribución que tiene Y. Estas no serán geométricamente distribuidas a menos que n = 1.

Distribuciones relacionadas

La distribución geométrica es un caso especial de la distribución binomial negativa con parámetro k = 1. Más generalmente, si Y ₁,...,Y_k son variables independientes distribuidas geométricamente con parámetro p, entonces $Z = sum_{m=1}^k Y_m$ sigue a una distribución binomial negativa con parámetros k y p.

Si Y₁,...,Y_r son variables independientes distribuidas geométricamente (con diferentes parámetros de éxito p_m posibles ), entonces su mínimo $W = min m Y m$ es también geométricamente distribuido, con parámetro

p = 1 −	∏	(1 − p_m)
	m

5.- Distribución hipergeométrica

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Distribución hipergeométrica
Función de distribución de probabilidad
Parámetros	$begin{align}N&in 0,1,2,dots m&in 0,1,2,dots,N n&in 0,1,2,dots,Nend{align},$
Dominio	$scriptstyle{k, in, max{(0,, n+m-N)},, dots,, min{(m,, n )}},$
Función de probabilidad (fp)	${{{m choose k} {{N-m} choose {n-k}}}over {N choose n}}$
Función de distribución (cdf)
Media	$n mover N$
Mediana
Moda	$left lfloor frac{(n+1)(m+1)}{N+2} right rfloor$
Varianza	$n(m/N)(1-(m/N))(N-n)over (N-1)$
Coeficiente de simetría	$frac{(N-2m)(N-1)^frac{1}{2}(N-2n)}{[nm(N-m)(N-n)]^frac{1}{2}(N-2)}$
Curtosis	$left[frac{N^2(N-1)}{n(N-2)(N-3)(N-n)}right]$ $cdotleft[frac{N(N+1)-6N(N-n)}{m(N-m)}right.$ $+left.frac{3n(N-n)(N+6)}{N^2}-6right]$
Entropía
Función generadora de momentos (mgf)	$frac{{N-m choose n} scriptstyle{,_2F_1(-n, -m; N - m - n + 1; e^{t}) } } {{N choose n}} ,!$
Función característica	$frac{{N-m choose n} scriptstyle{,_2F_1(-n, -m; N - m - n + 1; e^{it}) }} {{N choose n}}$

En teoría de la probabilidad la distribución hipergeométrica es una distribución discreta relacionada con muestreos aleatorios y sin reemplazo. Supóngase que se tiene una población de N elementos de los cuales, d pertenecen a la categoría A y N-d a la B. La distribución hipergeométrica mide la probabilidad de obtener x (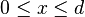 $0 le x le d$ ) elementos de la categoría A en una muestra de n elementos de la población original.

Propiedades

La función de probabilidad de una variable aleatoria con distribución hipergeométrica puede deducirse a través de razonamientos combinatorios y es igual a

$P(X=x)=frac{{d choose x}{{N-d choose n-x}}}{{N choose n}},$

donde $N$ es el tamaño de población, $n$ es el tamaño de la muestra extraída
, $d$ es el número de elementos en la población original que pertenecen a la
categoría deseada y $x$ es el número de elementos en la muestra que pertenecen
a dicha categoría. La notación 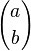${a choose b}$ hace referencia al coeficiente binomial,
es decir, el número de combinaciones posibles al seleccionar $b$ elementos de un total $a$ .

El valor esperado de una variable aleatoria X que sigue la distribución hipergeométrica es

$E[X]=frac{nd}{N}$

y su varianza,

$Var[X]=bigg(frac{N-n}{N-1}bigg)bigg(frac{nd}{N}bigg)bigg( 1-frac{d}{N}bigg).$

En la fórmula anterior, definiendo

$p = frac{d}{N}$

$q = 1-p,,$

se obtiene

$Var[X]=npqfrac{N-n}{N-1}.$

La distribución hipergeométrica es aplicable a muestreos sin reemplazo y
la binomial a muestreos con reemplazo. En situaciones en las que el número
esperado de repeticiones en el muestreo es presumiblemente bajo, puede
aproximarse la primera por la segunda. Esto es así cuando N es grande y
el tamaño relativo de la muestra extraída, n/N, es pequeño.

6.-Distribución de Bernoulli

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Bernoulli
Función de distribución de probabilidad
Parámetros	$0<p<1, pinR$
Dominio	$k={0,1},$
Función de probabilidad (fp)	$begin{matrix} q=(1-p) & mbox{para }k=0 p~~ & mbox{para }k=1 end{matrix}$
Función de distribución (cdf)	$begin{matrix} 0 & mbox{para }k<0 q & mbox{para }0leq k<11 & mbox{para }kgeq 1 end{matrix}$
Media	$p,$
Mediana	N/A
Moda	$begin{matrix} 0 & mbox{si } q > p 0 y 1 & mbox{si } q=p 1 & mbox{si } q < p end{matrix}$
Varianza	$pq,$
Coeficiente de simetría	$frac{q-p}{sqrt{pq}}$
Curtosis	$frac{6p^2-6p+1}{p(1-p)}$
Entropía	$-qln(q)-pln(p),$
Función generadora de momentos (mgf)	$q+pe^t,$
Función característica	$q+pe^{it},$

En teoría de probabilidad y estadística, la distribución de Bernoulli (o distribución dicotómica), nombrada así por el matemático y científico suizo Jakob Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito ( $p$ ) y valor 0 para la probabilidad de fracaso ( $q = 1 - p$ ).

Si $X$ es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro $p$ .

$X ˜ B e (p)$

La fórmula será:

$f (x) = p x (1 - p) 1 - x$ con $x = {0,1}$

Su función de probabilidad viene definida por:

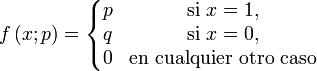
$fleft(x;pright) = left{begin{matrix} p & mbox {si }x=1, q & mbox {si }x=0, 0 & mbox {en cualquier otro caso}end{matrix}right.$

Un experimento al cual se aplica la distribución de Bernoulli se conoce
como Ensayo de Bernoulli o simplemente ensayo, y la serie de esos
experimentos como ensayos repetidos.

Propiedades características

Esperanza matemática:

$Eleft[Xright] = p$

Varianza:

$varleft[Xright] = p left(1 - pright) = p q$

Función generatriz de momentos:

$left( q + p e^{t} right)$

Función característica:

$left( q + p e^{i t} right)$

Moda:

0 si q > p (hay más fracasos que éxitos)

1 si q < p (hay más éxitos que fracasos)

0 y 1 si q = p (los dos valores, pues hay igual número de fracasos que de éxitos)

Asimetría (Sesgo):

$gamma_1 = frac{q - p}{ sqrt{q p} }$

Curtosis:

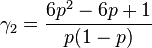
$gamma_2 = frac{6p^2-6p+1}{p(1-p)}$

La Curtosis tiende a infinito para valores de $p$ cercanos a 0 ó a 1, pero
para 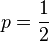$p=frac{1}{2}$ la distribución de Bernoulli tiene un valor de curtosis menor que el de cualquier otra distribución, igual a -2.

Distribuciones Relacionadas

Si 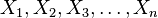$X_1, X_2, X_3, dots ,X_n$ son $n$ variables aleatorias identicamente distribuidas con la distribución de Bernoulli con la misma probabilidad de éxito $p$ en todas, entonces la variable aleatoria $X = X_1 + X_2 + dots + X_n$ presenta una Distribución Binomial de probabilidad.

$X ˜ B i (n, p)$

Ejemplo

"Lanzar una moneda, probabilidad de conseguir que salga cruz".

Se trata de un solo experimento, con dos resultados posibles: el éxito (p) se considerará sacar cruz. Valdrá 0,5. El fracaso (q) que saliera cara, que vale (1 - p) = 1 - 0,5 = 0,5.

La variable aleatoria X medirá "número de cruces que salen en un lanzamiento", y sólo existirán dos resultados posibles: 0 (ninguna cruz, es decir, salir cara) y 1 (una cruz).

Por tanto, la v.a. X se distribuirá como una Bernoulli, ya que cumple todos los requisitos.

$X ˜ B e (0,5)$

$P (X = 0) = f (0) = 0,5 0 0,5 1 = 0,5$

$P (X = 1) = f (1) = 0,5 1 0,5 0 = 0,5$

Ejemplo:

"Lanzar un dado y salir un 6".

Cuando lanzamos un dado tenemos 6 posibles resultados:

$Ω = {1,2,3,4,5,6}$

Estamos realizando un único experimento (lanzar el dado una sola vez).

Se considera éxito sacar un 6, por tanto, la probabilidad según el teorema de Laplace (casos favorables dividido entre casos posibles) será 1/6.

$p = 1 / 6$

Se considera fracaso no sacar un 6, por tanto, se considera fracaso sacar cualquier otro resultado.

$q = 1 - p = 1 - 1 / 6 = 5 / 6$

La variable aleatoria X medirá "número de veces que sale un 6", y solo existen dos valores posibles, 0 (que no salga 6) y 1 (que salga un 6).

Por tanto, la variable aleatoria X se distribuye como una Bernoulli de parámetro $p$ = 1/6

$X ˜ B e (1 / 6)$

La probabilidad de que obtengamos un 6 viene definida como la probabilidad de que X sea igual a 1.

$P (X = 1) = f (1) = (1 / 6) 1 * (5 / 6) 0 = 1 / 6 = 0.1667$

La probabilidad de que NO obtengamos un 6 viene definida como la probabilidad de que X sea igual a 0.

$P (X = 0) = f (0) = (1 / 6) 0 * (5 / 6) 1 = 5 / 6 = 0.8333$

7.-Distribución uniforme discreta

distribución uniforme discreta es una distribución de probabilidad que asume un número finito de valores con la misma probabilidad.

Propiedades

Distribución uniforme (caso discreto).

Si la distribución asume los valores reales $x_1, x_2ldots x_n ,!$ , su función de probabilidad es

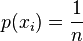
$p(x_i)=frac{1}{n} ,!$

y su función de distribución la función escalonada

$F(x)=frac{1}{n} sum_i 1_{(-infty,x]}(x_i),!.$

Su media estadística es

$mu=sum_{i}^n x_i/n ,!$

y su varianza

$sigma^2=sum_{i}^n (x_i-mu)^2/n ,!$

Ejemplos

Para un dado perfecto, todos los resultados tienen la misma probabilidad 1/6. Luego, la probabilidad de que al lanzarlo caiga 4 es 1/6.
Para una moneda perfecta, todos los resultados tienen la misma probabilidad 1/2. Luego, la probabilidad de que al lanzarla caiga cara es 1/2.

DISTRIBUCIONES DE LA VARIABLE DISCRETA

Y, tal como corresponde a la definición de distribución de probabilidad, esta expresión representa la suma de todas las probabilidades desde hasta el valor x.

1.- Distribución binomial

Ejemplos

Experimento Binomial

Características analíticas

Ejemplo

Propiedades características

Relaciones con otras variables aleatorias

Propiedades reproductivas

2.- Distribución binomial negativa

Propiedades

Ejemplos

3.- Distribución de Poisson

Propiedades

Relación con otras distribuciones

Sumas de variables aleatorias de Poisson

Distribución binomial

Aproximación normal

Distribución exponencial

Ejemplos

Procesos de Poisson

4.-Distribución geométrica

Propiedades

Distribuciones relacionadas

5.- Distribución hipergeométrica

Propiedades

6.-Distribución de Bernoulli

Propiedades características

Distribuciones Relacionadas

Ejemplo

7.-Distribución uniforme discreta

Propiedades

Ejemplos

DISTRIBUCIONES DE LA
VARIABLE DISCRETA

Y, tal como corresponde a la definición de distribución de probabilidad, esta expresión representa la suma de todas las probabilidades desde $-infty$ hasta el valor $x$ .